第十四届蓝桥杯 b组 省赛 E;
试题 E: 接龙数列
【问题描述】
对于一个长度为 K 的整数数列: A1, A2, . . . , A K,我们称之为接龙数列当且仅当 A i 的首位数字恰好等于 A i−1 的末位数字 (2 ≤ i ≤ K)。例如 12, 23, 35, 56, 61, 11 是接龙数列;12, 23, 34, 56 不是接龙数列,因为 56的首位数字不等于 34 的末位数字。所有长度为 1 的整数数列都是接龙数列。现在给定一个长度为 N 的数列 A1, A2, . . . , A N,请你计算最少从中删除多少个数,可以使剩下的序列是接龙序列?
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, . . . , A N。
【输出格式】
一个整数代表答案。
【样例输入】
5
11 121 22 12 2023
【样例输出】
1
【思路】
这道题目要求的是最少从中删除多少个数,而且没有询问我们是删除哪些数字,那就可以把问题转换为这个数列中最多有多少个接龙子序列,对于每一个数字我们也可以抽象成开头数字还有结尾数字,分别使用两个数组来存储就好,再来一个数组记录取到这一个整数最多能有多少个接力哦那个数列,然后从前往后一位一位枚举就好。
【代码】
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
typedef long long LL;
int a[N],b[N],dp[N];
int main()
{
int n;
cin>>n;
for(int i=0;i<n;++i)
{
int shuru;
cin>>shuru;
b[i]=shuru%10;
while(shuru>10)shuru/=10;
a[i]=shuru;
}
int maxzhi=0;
for(int i=0;i<n;++i)
{
dp[i]=1;
for(int j=0;j<i;++j)
{
if(b[j]==a[i])dp[i]=max(dp[i],dp[j]+1);
}
maxzhi=max(maxzhi,dp[i]);
}
cout<<n-maxzhi;
return 0;
}
/*
5
11 121 22 12 2023
*/试题 G: 子串简写
【问题描述】
程序猿圈子里正在流行一种很新的简写方法:对于一个字符串,只保留首尾字符,将首尾字符之间的所有字符用这部分的长度代替。例如 internation alization 简写成 i18n, Kubernetes (注意连字符不是字符串的一部分)简写成 K8s, Lanqiao 简写成 L5o 等。在本题中,我们规定长度大于等于 K 的字符串都可以采用这种简写方法 (长度小于 K 的字符串不配使用这种简写)。给定一个字符串 S 和两个字符 c1 和 c2,请你计算 S 有多少个以 c1 开头 c2 结尾的子串可以采用这种简写?
【输入格式】
第一行包含一个整数 K。
第二行包含一个字符串 S 和两个字符 c1 和 c2。
【输出格式】
一个整数代表答案。
【样例输入】
4
abababdb a b
【样例输出】
6
【G题答案】
这道题也是可以用DP解决的,因为本题只要求输出个数
我们对字符串从后往前,定义dp[i]表示字符串从i到字符串末尾len即 [ i,len ] 区间中c2的个数
状态转移方程:
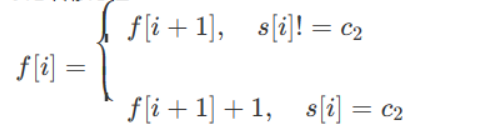
ans则是 [ 1, len-k+1 ]区间中所有当 s[i]=c1 时的 f[ i+k-1 ] 的和
即当s[i] = c1时,ans+= f[ i+k-1 ](从i+k-1到len的区间内c2的个数)
【代码实现】
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e5 + 5;
int k;
string s;
char c1, c2;
int f[N];
ll ans;
int main() {
cin >> k >> s >> c1 >> c2;
int len = s.size();
s = " " + s;
for (int i = len; i >= 1; i--) {//从后往前遍历,累加c2的个数,并存储在相应的位置上
f[i] = f[i + 1];
if (s[i] == c2) f[i] = f[i + 1] + 1;
}
for (int i = 1; i + k - 1 <= len; i++) {//只需找到离c1最近的符合条件的c2的f[]值,就能得到该c1的全部个数
if (s[i] == c1) ans += f[i + k - 1];
}
cout << ans;
return 0;
}




Comments NOTHING