关于深度优先搜索（DFS）

二叉数的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

DFS(深度优先)
关键点有：
1：理解Tree的构成，Tree的构成是利用递归去实现和定义的。
2：使用递归算法来检查Tree的深度
3：特殊条件当root结点为空时，应该返回0
时间复杂度：O(n)
空间复杂度：O(1)

//递归判断
int get_tree_depth(struct TreeNode* node)
{
    int rightDepth = 1;
    int leftDepth  = 1;
    //查找左子树
    if(node->left != NULL)
    {
        leftDepth = rightDepth + get_tree_depth(node->left);
    }

    //查找右子树
    if(node->right != NULL)
    {
        rightDepth = rightDepth + get_tree_depth(node->right) ;
    }

    if(leftDepth >= rightDepth)
    {
        return leftDepth;
    }
    else
    {
        return rightDepth;
    }
    
}

int maxDepth(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    return get_tree_depth(root);
}

优化后

int getTreeDepth(struct TreeNode* node)
{
    //结束条件
    if(node == NULL)
    {
        return 0;
    }
    int maxdDeep = 0;
    maxdDeep = fmax(maxdDeep ,getTreeDepth(node->left) + 1 );
    maxdDeep = fmax(maxdDeep ,getTreeDepth(node->right) + 1 );
    return maxdDeep;
}

int maxDepth(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    return getTreeDepth(root);
}

路径总和

题目描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

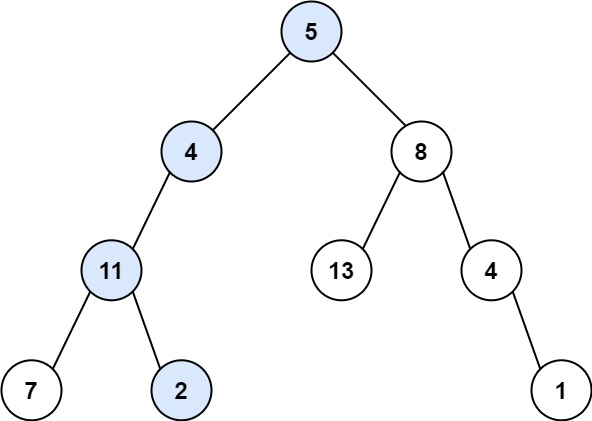
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22

输出：true

解释：等于目标和的根节点到叶节点路径如上图所示。

bool hasPathSum(struct TreeNode *root, int sum) {
    if (root == NULL) {
        return false;
    }
    if (root->left == NULL && root->right == NULL) {
        return sum == root->val;// 这个return有意思
    }
    return hasPathSum(root->left, sum - root->val) ||
           hasPathSum(root->right, sum - root->val);
}

n皇后问题

八皇后问题（英文：Eight queens），是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。
问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。
————————————————

                        版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/Genius_bin/article/details/116105020

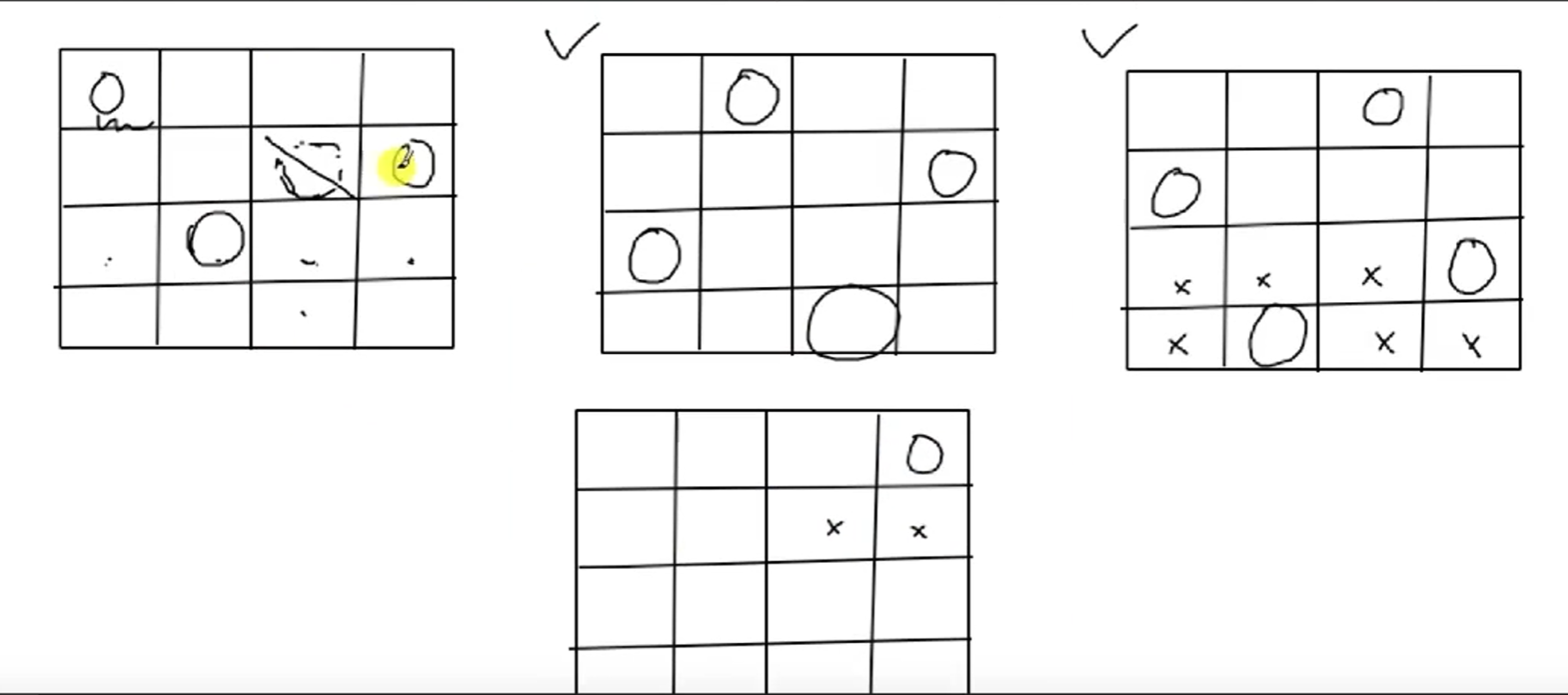
代码实现：

伪代码

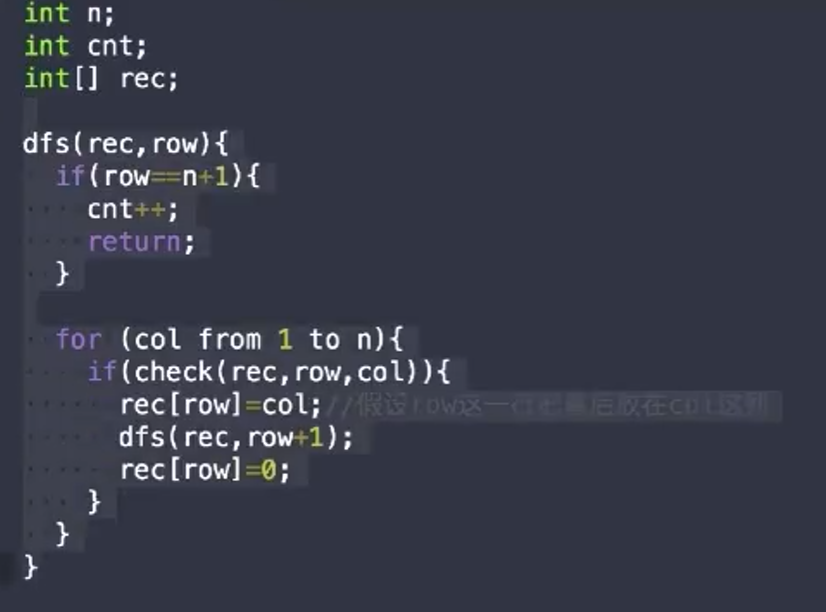
数组 rec[ ] 的下标表示为行，值表示为列号，就不需要二维数组了

check函数的伪代码

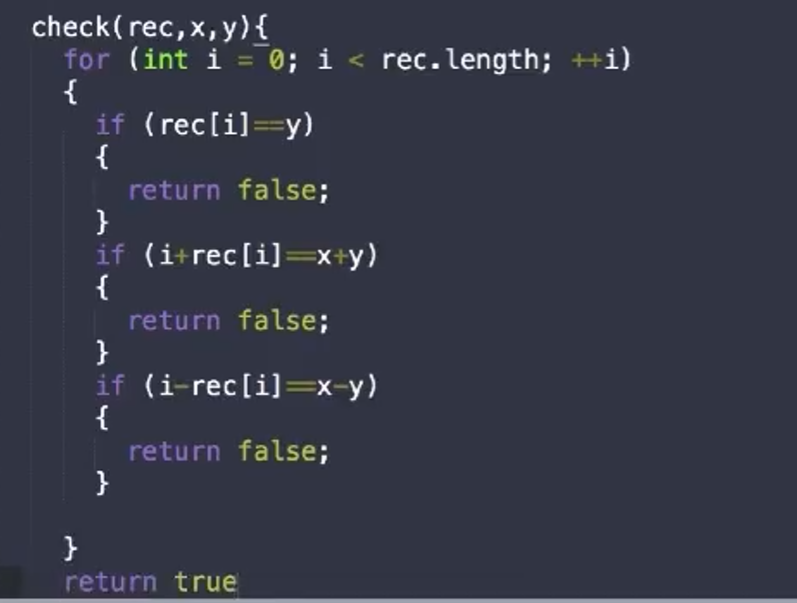
在主对角线上，x-y的值都相同，在负对角线上，x+y的值都相同

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>//C语言使用bool需要添加头文件
#define N 11
int a[N] = { 0 };
int ret;//函数中可以使用全局变量，不用传参了

bool check(int x, int y) {
    for (int i = 1; i <= x; i++) {
        if (a[i] == y) return false;
        if (i + a[i] == x + y) return false;
        if (i - a[i] == x - y) return false;
    }
    return true;
}
void dfs(int hang,int n) {
    if (hang == n + 1) {
        ret++;
        return;
    }
    for (int i = 1; i <= n; i++) {//列
        if (check(hang, i)) {
            a[hang] = i;
            dfs(hang + 1,n);
            a[hang] = 0;
        }
    }
}
int main(int argc, char* argv[])
{
    // 请在此输入您的代码
    int n = 0;
    scanf("%d", &n);
    ret = 0;
    int row = 0;

    dfs(1,n);

    printf("%d", ret);
    return 0;
}

玩具蛇

原题地址：12.玩具蛇 - 蓝桥云课 (lanqiao.cn)

代码实现

#include <stdio.h>
#include <stdlib.h>

#define N 4

int arr[N][N] = { 0 }; // 用于记录方格是否被访问过
int cnt = 0;

void dfs(int x, int y)
{
    if (x < 0 || y < 0 || x >= N || y >= N || arr[x][y] != 0)
        return;
    
    arr[x][y] = 1; // 标记当前方格已被访问
    
    // 如果所有方格都已被访问，则增加方案数
    int all_visited = 1;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (arr[i][j] == 0) {
                all_visited = 0;
                break;
            }
        }
        if (!all_visited) break;
    }
    if (all_visited) {
        cnt++;
    }
    
    dfs(x + 1, y); // 向右
    dfs(x, y + 1); // 向上
    dfs(x - 1, y); // 向左
    dfs(x, y - 1); // 向下
    
    arr[x][y] = 0; // 回溯，恢复方格状态
}

int main()
{
    for (int x = 0; x < N; x++)
    {
        for (int y = 0; y < N; y++)
        {
            dfs(x, y);
        }
    }
    printf("%d", cnt);
    return 0;
}